电势差与电场强度的关系

两点 AB 之间的电势差 U_{AB} 定义为将电荷从 A 点移动到 B 点所需的功/电荷量。

并联是指将一端连接到另一端。 起点和终点是相同的。 因此，无论走哪条路，对于相同的电荷量，自始至终电场力所做的功都是相同的，比值当然也是相同的，即它们的电势差为相同。

更详细地说，我可能需要一些大学知识。 虽然本身并不难，但符号一看就吓人，但现场科普需要更多的空间。 如果你看不懂，那很正常。

在宏观电磁学中，麦克斯韦方程组才是老大，普通的集总电路只是一个特例。 具体方法我们稍后再说。

麦克斯韦方程组认为，变化的磁场会产生无自旋电场，其定量描述为

\oint_{L}^{}\vec{E}\cdot d\vec{l}=-\int_s\frac{\\vec{B}}{\ t}d\vec{S}

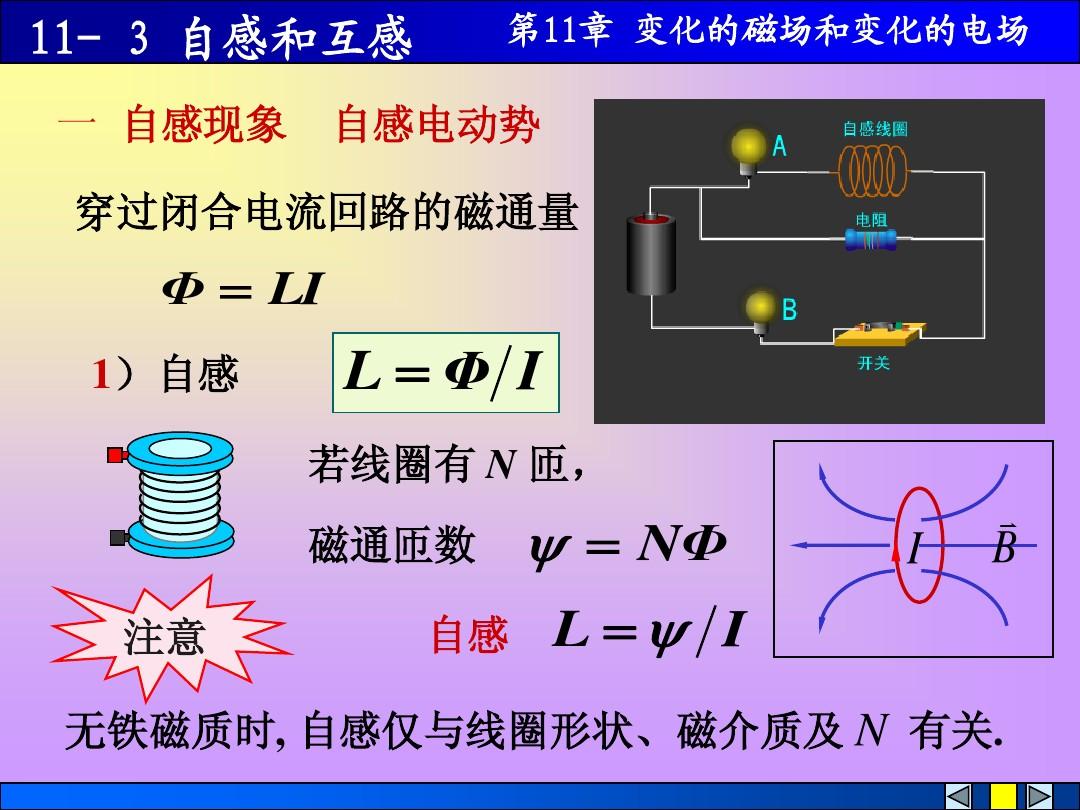
这意味着闭合路径L上电场强度E的环量等于通过曲面所包围的区域S的磁通变化率的负值。

如果一下子不能接受，就当成“随时间变化的磁场产生旋转电场”吧。 具体的关系可以从数量上翻译成专业的废话。

集总电路的要求之一是元件外部没有磁场。 （另外两种是没有外部电场且元件尺寸比工作波长小很多，这里关联不大，不再介绍。）

无磁场，磁感应强度B为0。上式简化为

\oint_{L}^{}\vec{E}\cdot d\vec{l}=0

从数学上来说，满足上式就相当于满足与路径无关的积分。 积分结果仅取决于起点和终点。

从物理角度来看，如果电场有旋转分量电势差与电场强度的关系，那么这个旋转分量就是由时变磁场产生的。

由于规定没有磁场，所以只有电荷本身向外辐射或向内聚集的电场。

对于这类没有旋转分量的场，一个结论是它们的功只与路径的起点和终点有关，而与路径无关。 （利用斯托克斯定理，用曲面上场旋度的通量来代替闭线上的环量。无旋场的旋度为0，可以直接推导出积分结果为0。路径积分结果为0。路径无关。）

那么回到一个弱智问题，什么是电压？

两点AB之间的电压定义为电荷在电场中从A点移动到B点时，电场力所做的功与电荷量的比值。

即 U_{AB}=\frac{W}{q}=\\int_a^b\vec{F}d\vec{l}

电场力与电场的关系为\vec{F}=q\vec{E}，因此可得 U_{AB}=\\int_a^bq\vec{E}d\vec{l}=\int_a ^b\ vec{E}d\vec{l}电势差与电场强度的关系，刚刚证明了这个东西在集总电路中是路径无关的。

到了这里，就是我们熟悉的剧情了

对于闭合路径，假设路径L被分成两段L1和L2，即两段并联连接。

在A点，无论是通过L1直接到达B点，还是通过ADCB到达B点，起点和终点都是相同的。因为路径无关，所以总有

\int_{L1}^{}\vec{E}\cdot d\vec{l}=\int_{L2}^{}\vec{E}\cdot d\vec{l}=U_{AB}