等腰三角形面积算法

等腰三角形面积公式

等腰三角形的面积计算公式为：s=(1/2)×底×高。等腰三角形（ ）是指至少有两条边相等的三角形。这两条相等的边称为这种三角形的腰。

等腰三角形中，相等的两条边称为三角形的边，另一条边称为底边。两条边之间的夹角称为顶角，边与底边之间的夹角称为底角。等腰三角形的两个底角相等（简称“等边有等角”）。

等腰三角形知识点总结

等腰三角形是一种形状特殊的三角形，其特点是两条边相等，其中一个角为底角。等腰三角形是几何学中一种重要的三角形，其性质和特点被广泛应用于各个领域。本文将对等腰三角形的知识点进行归纳，以帮助读者更好地理解和掌握这一概念。

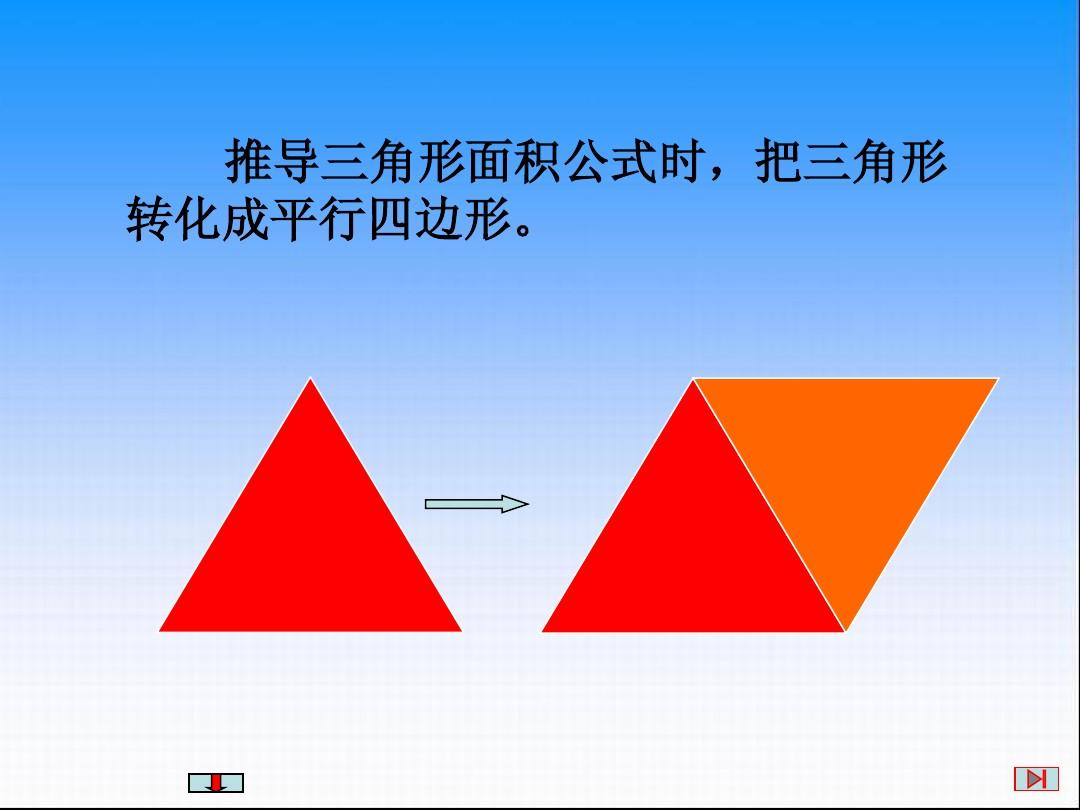
首先，我们需要明确等腰三角形的定义。等腰三角形是两条边相等的三角形，底角相等，顶角也相等。与三条边都相等的等边三角形不同等腰三角形面积算法，等腰三角形的三条边中只有两条相等。由于这种特殊的形状，等腰三角形在几何学中占有重要地位。

等腰三角形有许多重要的性质和特点。首先，由于它的两边相等，所以等腰三角形具有很高的对称性。在几何学中，对称性是一个重要的概念，是指图形在一定的变换下保持不变的性质。因此，等腰三角形的对称性使得它在几何学中有着广泛的应用。其次，由于等腰三角形的底角相等，所以它们的高也相等。这是很多几何问题中非常重要的性质。此外，等腰三角形还有许多其他的性质，如腰部的中线与底边的高重合等。

在实际应用中，等腰三角形有许多重要的应用领域。例如，在几何学中，等腰三角形经常被用来证明一些重要的定理和性质。在建筑学中，等腰三角形经常被用来设计一些形状特殊的建筑物，例如金字塔、角楼等。在物理学中，等腰三角形经常被用来描述一些物理现象，例如力学、光学等。此外等腰三角形面积算法，在航海、测量等领域，等腰三角形也有着广泛的应用。

在使用等腰三角形时，需要注意一些细节和注意事项。首先，需要明确等腰三角形的定义和性质，避免产生误解和错误。其次，需要正确画等腰三角形，注意等腰三角形的对称性和底角相等的性质。此外，还需要注意等腰三角形的应用领域和实际情况，才能正确运用等腰三角形的性质和特点。

综上所述，等腰三角形是一种特殊的三角形，具有许多重要的性质和特征，被广泛应用于各个领域。在实际应用中，需要注意一些细节和注意事项，才能正确运用其性质和特征。希望本文的总结可以帮助读者更好地理解和掌握等腰三角形的概念。

等腰三角形的三个角分别是多少度？

等腰直角三角形的三个角的度数分别为：90度、45度、45度。等腰三角形是至少有两条边相等的三角形。两条相等的边称为这个三角形的腰。在等腰三角形中，两条相等的边称为这个三角形的腰，另一条边称为底。两条腰之间的夹角称为顶角，腰与底之间的夹角称为底角。等腰三角形的两个底角度数相等（简称“等边有等角”）。